Lukion taulukot/Trigonometriset funktiot (Trigonometria)

Trigonometriset funktiot

Asteet ja radiaanit

Asteet	0	30	45	60	90	180	270	360	180 : π
Radiaanit	0	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$	$\frac{\pi }{2}$	$\pi$	$\frac{3\pi }{2}$	$2\pi$	1

Funktioiden määritelmät

$\sin \alpha =y$

$\cos \alpha =x$

$\tan \alpha =\frac{y}{x}=\frac{\sin \alpha }{\cos \alpha },\alpha \ne \frac{\pi }{2}+n\cdot \pi$

$\cot \alpha =\frac{x}{y}=\frac{\cos \alpha }{\sin \alpha }=\frac{1}{\tan \alpha },\alpha \ne n\cdot \pi$

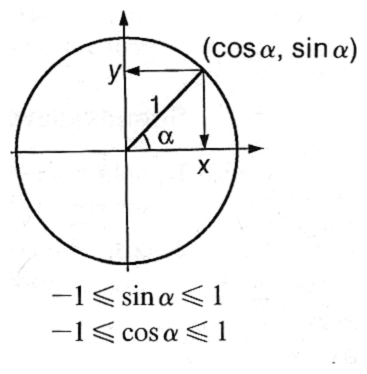
Peruskaavat

1.	${\sin }^{2}x+{\cos }^{2}x=1$
	$\sin x=\pm \sqrt{1-{\cos }^{2}x}$
	$\cos x=\pm \sqrt{1-{\sin }^{2}x}$
	${\sin }^{2}x=\frac{1-\cos 2x}{2}$
	${\cos }^{2}x=\frac{1+\cos 2x}{2}$
2.	$\sin (\frac{\pi }{2}-x)=\cos x$
	$\cos (\frac{\pi }{2}-x)=\sin x$
3.	$\tan (\frac{\pi }{2}-x)=\cot x$
	$\cot (\frac{\pi }{2}-x)=\tan x$
4.	$\sin x=\pm \frac{\tan x}{\sqrt{1+{\tan }^{2}x}};\cos x=\pm \frac{1}{\sqrt{1+{\tan }^{2}x}}$

Jaksollisuus

$\sin (x+n\cdot 2\pi )=\sin x$	perusjakso $2\pi$
$\cos (x+n\cdot 2\pi )=\cos x$
$\tan (x+n\cdot \pi )=\tan x$	perusjakso $\pi$
$\cot (x+n\cdot \pi )=\cot x$

Palautuskaavat

1.	$\sin (-x)=-\sin x$	vastakulmat
	$\cos (-x)=\cos x$
	$\tan (-x)=-\tan x$
2.	$\sin (\pi -x)=\sin x$	suplementtikulmat
	$\cos (\pi -x)=-\cos x$
	$\tan (\pi -x)=-\tan x$
3.	$\sin (\pi +x)=-\sin x$
	$\cos (\pi +x)=-\cos x$

Summakaavoja

1.	$\sin (x+y)=\sin x\cos y+\cos x\sin y$
	$\sin (x-y)=\sin x\cos y-\cos x\sin y$
2.	$\cos (x+y)=\cos x\cos y-\sin x\sin y$
	$\cos (x-y)=\cos x\cos y+\sin x\sin y$

3.	$\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$
	$\tan (x-y)=\frac{\tan x-\tan y}{1+\tan x\tan y}$
4.	$\cot (x+y)=\frac{\cot x\cot y-1}{\cot y+\cot x}$
	$\cot (x-y)=\frac{\cot x\cot y+1}{\cot y-\cot x}$
5.	$\sin x+\sin y=2\sin \frac{x+y}{2}\cos \frac{x-y}{2}$
	$\sin x-\sin y=2\cos \frac{x+y}{2}\sin \frac{x-y}{2}$
6.	$\cos x+\cos y=2\cos \frac{x+y}{2}\cos \frac{x-y}{2}$
	$\cos x-\cos y=-2\sin \frac{x+y}{2}\sin \frac{x-y}{2}$

Kaksinkertaiset ja puolet kulmat

1.	$\sin 2x=2\sin x\cos x$
2.	$\cos 2x={\cos }^{2}x-{\sin }^{2}x=2{\cos }^{2}x-1=1-2{\sin }^{2}x$
3.	$\tan 2x=\frac{2\tan x}{1-{\tan }^{2}x};\cot 2x=\frac{{\cot }^{2}x-1}{2\cot x}$
4.	$1+\cos x=2{\cos }^2\frac{1}{2}x;1-\cos x=2{\sin }^2\frac{1}{2}x$
5.	$1+\sin x=2{\sin }^2(\frac{\pi }{4}+\frac{1}{2}x)=2{\cos }^2(\frac{\pi }{4}-\frac{1}{2}x)$
6.	$1-\sin x=2{\sin }^2(\frac{\pi }{4}-\frac{1}{2}x)=2{\cos }^2(\frac{\pi }{4}+\frac{1}{2}x)$
7.	$\tan \frac{1}{2}x=\frac{\sin x}{1+\cos x}=\frac{1-\cos x}{\sin x}$